What Is Correlation and How It Can Protect Your Portfolio

Correlation is a statistical measure that describes how two securities move in relation to each other. For traders and investors in the US, UK, Canada, and Australia, understanding correlation is fundamental to building diversified portfolios that can weather market volatility and manage risk effectively.

Summary Table

Aspect	Detail
Definition	A statistical measure ranging from -1 to +1 that indicates the degree to which two assets move in tandem.
Also Known As	Pearson Correlation Coefficient, Asset Correlation
Main Used In	Portfolio Management, Risk Management, Quantitative Trading, Asset Allocation
Key Takeaway	Correlation is the cornerstone of diversification; combining assets with low or negative correlation can significantly reduce portfolio risk without necessarily sacrificing returns.
Formula	ρ = Cov(X,Y) / (σX * σY)
Related Concepts	Diversification Beta Covariance

What is Correlation

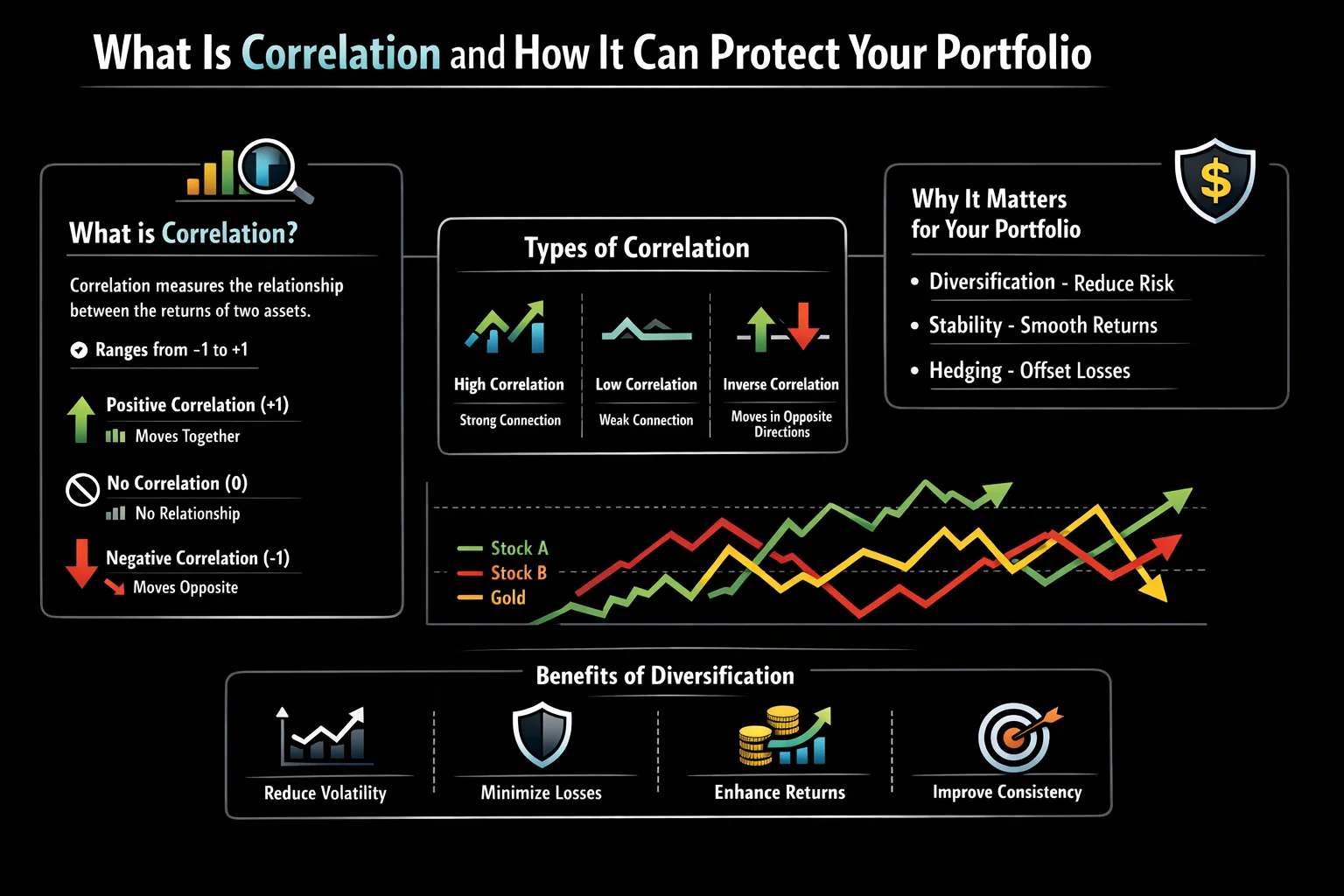
Correlation, specifically the Pearson correlation coefficient, quantifies the strength and direction of the linear relationship between two variables—in finance, these are typically the returns of two assets. Think of it not as a measure of causation, but of companionship. Do two stocks tend to rise and fall together, or does one zig when the other zags? Correlation answers this question with a precise number.

Imagine two dancers. A perfect positive correlation (+1) means they are perfectly in sync, moving together in every step. A perfect negative correlation (-1) means they are in a mirrored dance, moving in exactly opposite directions. A correlation of 0 means their movements are completely independent; one dancer’s steps have no predictable relation to the other’s.

Key Takeaways

Correlation measures the relationship between two assets, ranging from -1 (perfect negative) to +1 (perfect positive).

It is the bedrock of diversification; combining low or negatively correlated assets reduces overall portfolio volatility.

Correlation does not imply causation; two assets can move together without one causing the other’s movement.

Correlations are not static; they can and do break down, especially during market crises.

Understanding correlation helps in hedging strategies, allowing investors to offset potential losses in one position with gains in another.

The Core Concept Explained

Correlation measures the degree to which the price movements of two assets are related. The key is to interpret the number:

+1.0 (Perfect Positive Correlation): This means the two assets move in the same direction 100% of the time. If Asset A goes up 2%, Asset B also goes up 2%. An example would be two nearly identical tech stocks.
0.0 (No Correlation): There is no linear relationship between the assets. The movement of one provides zero insight into the movement of the other. Think of the relationship between the price of a stock and local weather patterns.
-1.0 (Perfect Negative Correlation): The two assets move in opposite directions 100% of the time. If Asset A goes up 3%, Asset B goes down 3%. This is rare but powerful for hedging.

In practice, you’ll rarely see perfect -1, 0, or +1. Most correlations fall somewhere in between. A correlation of +0.8 suggests a strong positive relationship, while -0.5 suggests a moderate negative relationship.

Beyond Pairs: The Correlation Matrix

In real-world portfolio management, you rarely deal with just two assets. This is where a correlation matrix becomes essential. It’s a table that shows the correlation coefficients between multiple assets in a portfolio. Reading it is simple: look at the intersection of row and column for any two assets. A well-diversified portfolio will have a matrix filled with many low or negative numbers, indicating that the assets don’t all move together.

Placement: Add this after the “Core Concept Explained” section to show the practical application of correlation in multi-asset portfolios.

How to Calculate Correlation

The most common formula used in finance is the Pearson Correlation Coefficient, represented by the Greek letter rho (ρ) or simply ‘r’.

Formula: ρ = Cov(X,Y) / (σX * σY)

Where:

Cov(X,Y) is the covariance between the returns of asset X and asset Y.
σX is the standard deviation of returns of asset X.
σY is the standard deviation of returns of asset Y.

Step-by-Step Calculation Guide

Let’s break down what this formula is doing:

Covariance: This measures how two assets move together. A positive covariance means they tend to move in the same direction, while a negative one means they move inversely.
Standard Deviation: This measures the volatility or dispersion of a single asset’s returns.
The Division: Dividing covariance by the product of the standard deviations normalizes the measure. This confines the result to a neat -1 to +1 scale, making it easily interpretable and comparable across different pairs of assets.

Example Calculation: Tech Stock vs. Utility Stock

Let’s calculate the 1-year daily return correlation between a hypothetical tech stock (X) and a utility stock (Y). We have 252 days of return data.

Step	Variable	Value (Hypothetical)
1	Covariance of X and Y (Cov(X,Y))	0.0004
2	Standard Deviation of X (σX)	0.018 (1.8%)
3	Standard Deviation of Y (σY)	0.009 (0.9%)
4	Product of σX and σY	0.018 * 0.009 = 0.000162
5	Correlation (ρ)	0.0004 / 0.000162 ≈ 0.247

Interpretation: A correlation of approximately +0.25 indicates a weak positive relationship. This makes intuitive sense: a volatile tech stock and a stable utility stock often react differently to market news, leading to a low correlation. This is a classic example of assets you might combine for diversification. For investors in the US, this is why pairing a NASDAQ-listed tech stock with a utility from the NYSE can be an effective strategy.

Why Correlation Matters to Traders and Investors

Correlation moves from an abstract statistical concept to a critical practical tool in several ways:

For Investors: This is the heart of Modern Portfolio Theory (MPT). By combining assets with low or negative correlations, an investor can create a portfolio that has a lower overall risk (volatility) than the weighted average risk of its individual components. For example, when stocks (S&P 500) are falling, bonds (U.S. Treasuries) have historically often risen, providing a cushion. This is the “holy grail” of portfolio construction—reducing risk without proportionally reducing expected returns.
For Traders: Traders use correlation to spot pairs trading opportunities, gauge market sentiment, and manage risk on multiple positions. If a trader is long on several tech stocks that are highly correlated, they are effectively taking a massive, concentrated bet on that single sector. Understanding this helps them size positions appropriately or find hedging instruments.
For Analysts: Correlation is used in more complex models, such as calculating the Beta of a stock, which measures its correlation and sensitivity to the broader market. It’s also crucial in valuing options and other derivatives where the relationship between multiple underlying assets is a key input.

How to Use Correlation in Your Strategy

Use Case 1: Building a Diversified Portfolio

Before adding a new asset to your portfolio, check its correlation with your existing holdings. For long-term investors in the UK, this might mean checking the correlation between a UK-focused FTSE 100 ETF and an international equity fund. A low correlation confirms the diversification benefit.

To easily check correlations, you need a platform with robust analytics. Many of the best online brokers for long-term investing offer these tools built into their research sections.

Use Case 2: Pairs Trading (A Statistical Arbitrage Strategy)

Identify two stocks in the same sector with a historically high correlation (e.g., Coca-Cola and Pepsi). If the correlation temporarily breaks down and one stock significantly underperforms the other, a pairs trader might short the outperformer and go long the underperformer, betting on the correlation (and their price spread) returning to its historical norm.

Use Case 3: Hedging with Negative Correlation

If you have a large portfolio of US stocks, you might be worried about a market downturn. You could buy put options on the S&P 500 (which have a strong negative correlation to the market during a crash) or allocate a portion to assets like gold or certain inverse ETFs, which often exhibit low or negative correlations with equities during stress periods.

Where to Find Correlation Data

You don’t need to calculate this by hand. Most professional platforms provide it.

TradingView: Use the “Correlation Coefficient” indicator on a chart.
Your Brokerage Platform: Many, like Fidelity or Charles Schwab, have built-in stock comparison tools that include correlation.
Free Online Tools: Sites like Portfoliovisualizer.com allow you to input multiple ETFs or stocks and generate a full correlation matrix over your chosen time frame.

How to Interpret a Real Correlation Matrix:

Step 1: Check the diagonal (it should be all 1s, as an asset is perfectly correlated with itself).
Step 2: Look for the highest positive numbers; these are your biggest concentration risks.
Step 3: Look for the lowest (or negative) numbers; these are your best diversifiers.
Placement: Add this after the “Practical Application” section to provide a direct, actionable “how-to” for readers.

Advantages of Correlation

Quantifies Diversification Provides a clear, numerical basis for the concept of “not putting all your eggs in one basket.”
Simple Interpretation The -1 to +1 scale is intuitive and easy to understand, even for beginners.
Foundation for Models A critical input for advanced concepts like portfolio optimization and Beta calculation.
Improves Risk Management Helps investors and managers avoid unintended risks by revealing hidden concentrations.

Limitations of Correlation

No Causation The biggest pitfall. A high correlation does not mean one asset’s movement causes the other’s.
Linear Only Only measures linear relationships, potentially missing complex non-linear relationships.
Dynamic & Unstable Correlations can break down, especially during market crises, reducing diversification benefits.
Time-Sensitive The value is highly dependent on the time frame and specific period selected for analysis.

Correlation in the Real World: The 2008 Financial Crisis

The 2008 Global Financial Crisis provides a stark lesson in correlation breakdown. In the years leading up to the crisis, the correlation between various asset classes (international stocks, different sectors, etc.) appeared manageable, allowing quants and portfolio managers to believe their models were sound.

However, when Lehman Brothers collapsed, it triggered a “flight to safety.” Suddenly, almost all risky assets—regardless of their country, sector, or fundamentals—plummeted in unison. The correlations between them spiked towards +1. The diversification that investors relied on vanished at the worst possible moment. This event forced a fundamental re-evaluation of risk models that relied on stable, long-term historical correlations. For a detailed analysis of this period, the Federal Reserve’s publications offer authoritative insights.

Conclusion

Ultimately, understanding correlation is non-negotiable for building resilient investment portfolios and executing sophisticated trading strategies. It provides the statistical backbone for the timeless wisdom of diversification. However, as we’ve seen, it is not a “set-and-forget” number. Its limitations—particularly its inability to prove causation and its tendency to shift during market turmoil—mean it must be used wisely. Correlation is a powerful lens for viewing market relationships, but it should be one tool among many in your analytical toolkit. Start by analyzing the correlations within your own portfolio; you might be surprised by the hidden concentrations of risk.

Ready to put these concepts into action? The right tools are essential. We’ve meticulously reviewed and ranked the best online brokers for technical analysis and long-term investing to help you get started.

How Correlation Relates to Other Concepts

Correlation is often confused with Covariance and Beta. Here’s how they differ.

Feature	Correlation	Covariance	Beta (β)
What it measures	Strength & direction of a linear relationship.	Direction of the linear relationship (but not standardized).	Sensitivity of a stock’s returns to the market’s returns.
Scale/Range	-1 to +1	-∞ to +∞	Typically around -2 to +2, but unbounded.
Interpretation	Easy (standardized).	Difficult (not standardized; depends on units).	Intuitive (e.g., β = 1.2 → 20% more volatile than market).
Primary Use	Diversification; assessing relationship strength.	Used to calculate correlation & Beta.	Gauging a stock’s market risk; used in CAPM.

Related Terms

Diversification: The strategy of using low correlation to reduce risk.
Beta: Beta is essentially the correlation of a stock to the market, multiplied by the ratio of their volatilities. It’s a special case of correlation.
Modern Portfolio Theory (MPT): The foundational academic theory that uses correlation to construct optimal portfolios.
Covariance: The unstandardized precursor to the correlation calculation.
R-Squared (R²): In regression, this tells you how much of the movement in one asset can be explained by the movement of another; it’s the square of the correlation coefficient.

Frequently Asked Questions

Can correlation help me predict the future price of a stock?

No, correlation is a backward-looking statistical measure. It describes historical relationships but does not predict future movements. Relying on it for precise price predictions is a mistake. The relationship can change due to new market conditions, rendering past correlations useless for forecasting.

I’ve found two assets with a near-perfect negative correlation. Is this a guaranteed, risk-free profit opportunity?

Not at all. While it seems like a perfect hedge, it’s extremely rare and often temporary. There’s no guarantee the relationship will persist. Furthermore, transaction costs, borrowing fees (for shorting), and timing risks can easily erase any theoretical profit. It’s a powerful risk-reduction tool, not a risk-free profit machine.

How often should I check the correlations in my portfolio?

For a long-term investor, a quarterly or semi-annual review is sufficient. For active traders or those using strategies highly dependent on specific correlations (like pairs trading), monitoring should be much more frequent—weekly or even daily. The key is to be aware that correlations are dynamic.

What’s a “good” or “bad” correlation for portfolio diversification?

There’s no single magic number, but generally, a correlation below +0.5 is considered beneficial for diversification. The ideal is to find assets with strong return potential but correlations as low as possible, or even negative. A correlation above +0.8 suggests high overlap and little diversification benefit.

Are there different types of correlation coefficients?

Yes. The Pearson coefficient (covered here) measures linear relationships. Another important type is Spearman’s Rank Correlation, which measures monotonic relationships (whether the relationship is consistently increasing or decreasing, even if not in a straight line). Spearman’s is more robust to outliers.

Recommended Resources

The CFA Institute provides deep, practitioner-level insights into correlation and its role in portfolio management.
Investopedia’s entry on Correlation offers a great refresher and further examples.
Portfoliovisualizer.com is an excellent free tool to backtest portfolio asset allocation and view historical correlation matrices for US-listed ETFs and stocks.

Muhammad Faraz

Administrator

Faraz breaks down stocks, forex, commodities, and crypto with technical analysis, spotting key trends and trades daily. He specializes in technical and sentiment analysis, decoding complex market trends across crypto, forex, and stocks. With a sharp eye for key levels and breakout patterns, he transforms data into actionable trade setups.

Author's website Author's posts