What Is Delta in Options Trading and How to Use It

Delta is the foundational Greek in options trading, measuring how much an option’s price is expected to change for every $1 move in the underlying asset. It’s the market’s best estimate of an option finishing in-the-money and serves as a crucial hedge ratio for managing portfolio risk. Mastering delta is the first step to transitioning from a speculative trader to a strategic risk manager.

For traders in the US, UK, Canada, and Australia, delta is a non-negotiable metric displayed on every major trading platform like Thinkorswim (Charles Schwab), Interactive Brokers, and CommSec. Understanding it is essential for navigating markets like the NYSE, NASDAQ, and ASX.

Summary Table

Aspect	Detail
Definition	Delta measures the rate of change in an option’s price relative to a $1 change in the price of the underlying asset.
Also Known As	Hedge Ratio, Probability Delta
Main Used In	Options Trading, Portfolio Hedging, Risk Management
Key Takeaway	It quantifies both directional risk and the estimated probability of an option expiring in-the-money.
Formula	Δ = ΔOption / ΔUnderlying
Related Concepts	Gamma Theta Vega Black-Scholes Model

What is Delta

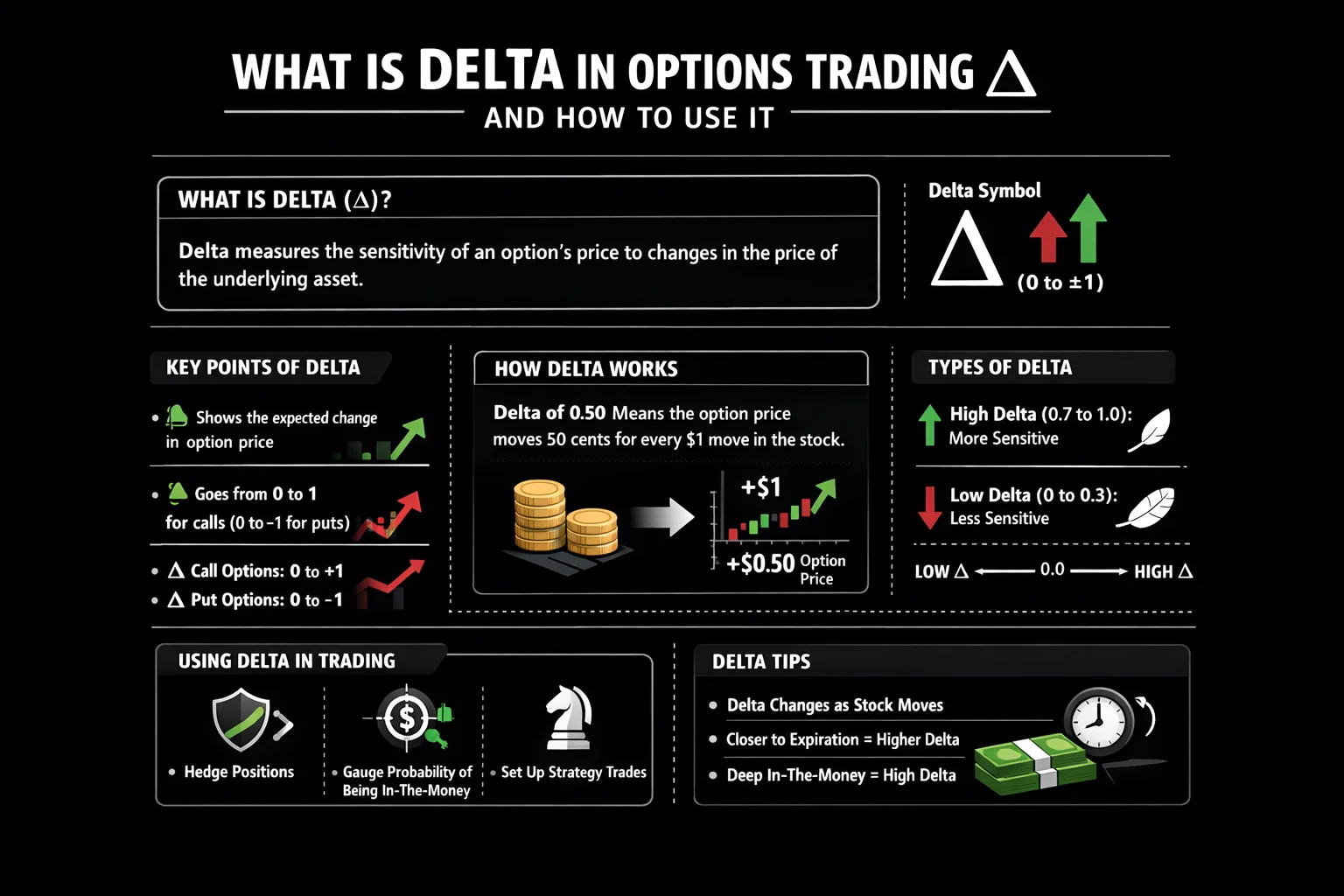
Delta (Δ) is more than just a number; it’s a dynamic gauge of an option’s sensitivity. Think of it as the speedometer for your option’s price. If you own a call option with a delta of 0.60, your option’s price will theoretically increase by $0.60 for every $1 increase in the stock price. Conversely, it will lose $0.60 if the stock drops by $1. For put options, delta is negative, typically ranging from -1 to 0, indicating the option gains value when the underlying asset falls.

Beyond price sensitivity, delta is famously interpreted as the approximate probability of that option expiring in-the-money. A call delta of 0.75 suggests roughly a 75% chance the option will finish above the strike price at expiration. This probability aspect makes it a critical tool for assessing trade viability.

<<<<<<<<<<<<>>>>>>>>>>>>>>>>

Key Takeaways

Directional Gauge: Delta measures an option’s price sensitivity to the underlying asset’s moves. Positive delta (calls) benefits from price rises; negative delta (puts) benefits from price declines.

Hedge Ratio: Delta tells you how many shares of stock are needed to offset the price risk of an option (Delta Neutral Hedging).

Probability Estimate: It approximates the likelihood of an option expiring in-the-money (e.g., a 0.30 delta ≈ 30% probability).

Not Constant: Delta changes with the asset price, time, and volatility, a phenomenon measured by Gamma.

Portfolio Management: The net delta of an options portfolio reveals its overall directional bias and market risk.

The Core Concept Explained

Delta is a first-order derivative pricing sensitivity, derived from models like Black-Scholes. Its value isn’t static; it’s most sensitive when an option is at-the-money (ATM), typically around 0.50 for calls and -0.50 for puts. As an option moves deep in-the-money (ITM), its delta approaches 1.0 (or -1.0 for puts), meaning it moves nearly penny-for-penny with the stock, behaving like the underlying asset itself. Deep out-of-the-money (OTM) options have deltas near 0, as their price is largely unresponsive to small stock moves.

This behavior creates a curve, not a straight line. Gamma measures the rate of change of delta itself. Understanding this relationship is key: an ATM option with a 0.50 delta has the highest gamma, meaning its delta will change rapidly with stock movement, accelerating profits or losses.

How is Delta Calculated

While delta is automatically calculated by trading platforms, it stems from the Black-Scholes option pricing model. The formula for the delta of a European call option (no dividends) is:

Δ_call = N(d1)

Where:

N() is the cumulative distribution function of the standard normal distribution.
d1 is a variable within the Black-Scholes formula that incorporates the stock price, strike price, time to expiration, risk-free rate, and volatility.

For a put option:

Δ_put = N(d1) - 1

Understanding the Components

You don’t need to calculate this manually, but understanding the inputs shows what drives delta:

Underlying Price & Strike Price: Their relationship (ITM, ATM, OTM) is the primary driver.
Time to Expiration: More time generally pushes ATM option deltas toward 0.50, as there’s more uncertainty.
Implied Volatility (IV): Higher IV can increase the delta of OTM options and decrease the delta of ITM options, as extreme moves become more likely.
Risk-Free Rate & Dividends: Have a smaller, but mathematically defined, impact.

Example: Let’s look at Apple Inc. (AAPL) listed on the NASDAQ. If AAPL is trading at $175 and a 30-day $175 strike call option has a price of $6.00 and a delta of 0.55:

If AAPL rises to $176 (+$1), the call’s price would theoretically be ~$6.55.
This 0.55 delta also implies about a 55% chance this call expires in-the-money.
For a trader in the UK looking at an AstraZeneca (AZN) put option on the LSE with a delta of -0.40, a £1 drop in AZN would increase the put’s value by approximately £0.40.

Delta Across Different Asset Classes

Delta behaves uniquely across different underlying assets – a crucial nuance many guides overlook. Understanding these differences is key to effective risk management in diverse markets.

Equity Options

Standard behavior as described throughout this guide. American-style options allow early exercise, which can affect delta as options approach expiration, especially when dividends are involved.

✓ Most straightforward delta calculation
✓ Dividends significantly impact delta
✓ Early exercise possibility affects ITM deltas

Index Options (SPX, NDX)

Typically European-style (no early exercise), which simplifies delta calculation. However, they represent a basket of stocks, so their volatility dynamics differ from single stocks.

✓ No early exercise complications
✓ Cash-settled (no physical delivery)
✓ Lower dividend impact overall

Futures Options

Delta measures sensitivity to the futures contract price, not the spot price. Must account for cost of carry and convergence to spot price at expiration.

✓ Includes cost of carry factors
✓ High leverage amplifies delta effects
✓ Often more liquid than stock options

Special Cases Worth Noting:

Currency (FX) Options

Incorporate two interest rates (domestic and foreign), making delta hedging more complex. The Garman-Kohlhagen model, an extension of Black-Scholes, is typically used.

Crypto Options

Extremely high volatility leads to wider delta swings. The nascent market structure can create pricing dislocations from theoretical values, making delta hedging more challenging.

Key Insight: Always verify which pricing model your broker/platform uses for different asset classes, as this directly affects the delta calculation you see.

<<<<<<<<<<<<>>>>>>>>>>>>>>>>

Why Delta Matters to Traders and Investors

Delta translates abstract option theory into concrete risk management.

For Options Traders: It’s your direct exposure meter. A portfolio with a net delta of +300 is essentially bullish, with a risk profile similar to owning 300 shares of stock. Traders can adjust positions to achieve “delta neutrality,” temporarily insulating themselves from small market moves to profit from other factors like time decay or changes in volatility.
For Long-Term Investors: Delta provides a sophisticated hedging tool. An investor holding 1000 shares of a stock (delta +1000) can buy put options to protect against a downturn. If each put has a delta of -0.60, buying 17 puts gives a hedge delta of -1020 (~17 * 60), nearly offsetting the stock’s directional risk. This portfolio hedge strategy is central to protective collars.
For Risk Managers: It quantifies the “dollar delta” or “position delta”—the expected profit/loss for a 1% move in the market. This is fundamental for stress-testing portfolios.

<<<<<<<<<<<<>>>>>>>>>>>>>>>>

How to Use Delta in Your Trading Strategy

Use Case 1: Directional Bets with Managed Risk
Instead of buying 100 shares of XYZ at $50 ($5,000 capital), you could buy 2 call options with a 0.70 delta for $3.00 each ($600 total). Your “share-equivalent” exposure is 2 contracts * 100 shares * 0.70 delta = +140 delta. You get more leverage and defined risk (max loss $600), though you face time decay.

Use Case 2: Creating a Delta-Neutral Income Trade (Iron Condor)
Sell an OTM call spread and an OTM put spread on the same underlying with the same expiration. The goal is to structure the trade so the positive delta from the put side offsets the negative delta from the call side, resulting in a net delta near zero. The trader profits if the stock stays within a range, collecting premium from time decay (Theta).

Use Case 3: Dynamic Hedging (The “Gangnam Style” Hedge)
Imagine you sold a call option and are short delta. As the stock rises, your negative delta becomes more negative, increasing losses. To hedge, you must buy shares (positive delta) to re-balance. This is “dynamic hedging“—continuously buying high and selling low to remain delta-neutral, which is how market makers operate. It’s risky and transaction-heavy for retail traders.

To implement these strategies, you need a broker with robust options analytics and low fees. Platforms like Thinkorswim by Charles Schwab or Interactive Brokers provide advanced tools to monitor your portfolio’s live Greeks.

Advantages of Delta

Quantifies Risk: Transforms vague directional bias into a precise, numeric exposure.
Enables Hedging: The cornerstone of portfolio hedge strategies, allowing investors to tailor their market risk.
Probability Insight: Provides a quick, model-based estimate of an option’s success probability.
Foundation for Strategy: Essential for constructing multi-leg spreads where managing net delta is the goal.
Universal Language: A standardized metric used by all professional traders and risk systems.

Limitations of Delta

A Snapshot: It’s a momentary sensitivity, assuming other factors (volatility, time) are constant.
Gamma Risk: Delta’s change is the real danger. A small stock move can suddenly create a large, adverse position.
Model-Dependent: Relies on theoretical models (Black-Scholes) that have well-known flaws.
Misleading Probability: The “probability” interpretation can be inaccurate for far OTM options or during high-volatility events.
Incomplete Picture: Ignores other critical risks: time decay (Theta), volatility changes (Vega), and interest rates (Rho).

Advanced Delta Concepts: Charm, Color, and Beyond

Beyond basic delta lies a world of “higher-order Greeks” that measure how delta itself changes under various conditions. These are essential for professional traders managing complex portfolios.

Charm (Δ-Decay)

∂Δ/∂τ

The rate of change of delta with respect to time. Also called “delta decay,” this measures how an option’s delta evolves as expiration approaches, holding all else constant.

Real-World Impact:

For ATM Options: Charm is typically negative for calls and positive for puts as expiration nears, meaning ATM calls lose delta while ATM puts gain delta over time.
Weekend Effect: A trader holding a delta-neutral position over a weekend will see their delta exposure change due to charm – this is why many professionals adjust hedges on Friday afternoons.
Practical Use: Helps predict how much a delta hedge will need adjusting without any price movement in the underlying.

Charm Formula (Call Option):

Charm_call = -e^-qτ × [φ(d₁) × (σ/(2τ√τ)) + q × N(d₁)]

Where φ() is the normal PDF, N() is the normal CDF, q is dividend yield, τ is time to expiration, σ is volatility.

Color (Γ-Decay)

∂Γ/∂τ

The rate of change of gamma with respect to time. Also called “gamma decay” or “DgammaDtime,” this measures how quickly an option’s convexity changes as expiration approaches.

Trading Implications:

Gamma Scalpers: Professional market makers monitor color to anticipate how often they’ll need to re-hedge their delta-neutral positions.
Peak Gamma: Color helps identify when gamma (and thus hedging activity) will be highest – typically highest for ATM options with 7-14 days to expiration.
Risk Management: A high positive color means gamma is increasing rapidly with time – this dramatically increases hedging costs and risk for short option positions.

Professional Insight:

“Charm and color explain why delta-neutral positions aren’t ‘set and forget.’ A market maker who is delta-neutral at 4 PM Friday might wake up Monday with significant delta exposure even if the stock hasn’t moved. This ‘theta-induced delta’ is what charm measures.”

Practical Applications for Retail Traders

🔄

Hedge Timing

Understanding charm helps determine optimal times to adjust hedges. Most charm occurs in the final week before expiration.

📊

Position Selection

Options with high color will require more frequent adjustments – important for traders with limited time or high transaction costs.

⚖️

Risk Assessment

These metrics reveal hidden risks in seemingly neutral positions, especially over weekends and holidays.

Note: Most retail platforms don’t display charm and color directly. Professional platforms like Bloomberg, Reuters Eikon, or specialized options analytics software provide these metrics. However, understanding their existence makes you a more sophisticated trader.

<<<<<<<<<<<<>>>>>>>>>>>>>>>>

Delta in the Real World

A powerful example of delta and gamma’s real-world impact was the “Volmageddon” event of February 2018 and similar gamma squeezes seen during the 2020 market recovery. Here’s how delta was central:

The Setup: After a long period of low volatility, hundreds of billions of dollars were invested in short volatility ETF products (like SVXY) and strategies that involved selling OTM put options.
The Trigger: A sudden, sharp market drop (like the COVID-19 crash) caused implied volatility to spike. The delta of those previously safe, OTM puts skyrocketed from near 0 to much higher negative values (e.g., from -0.10 to -0.70).
The Gamma Squeeze: As delta became more negative, the institutions that had sold these puts were suddenly exposed to massive directional risk (short the market). To hedge this risk and remain delta-neutral, they were forced to dynamically hedge by SELLING shares of the underlying stocks (S&P 500 constituents). This institutional selling pressure accelerated the market’s decline, which further increased the delta of the puts, forcing even more selling—a vicious feedback loop known as a “gamma squeeze.”

This case study shows that delta isn’t just a theoretical metric; its dynamic hedging implications can move entire markets.

Delta-Based Trading Strategies: From Theory to Practice

Delta isn’t just a metric – it’s the foundation for systematic trading approaches. Here are three professional-grade strategies that use delta as their primary decision-making tool.

Delta-Neutral Trading

Gamma Scalping

Core Concept

Construct positions with net delta ≈ 0 to profit from changes in volatility or time decay, while minimizing directional risk. The goal is to be “market neutral.”

Implementation

ATM Straddle/Strangle: Buy both call and put at/near same strike(s) for delta ≈ 0
Iron Condor: Sell OTM call spread + OTM put spread, balanced for delta neutrality
Calendar Spread: Sell near-term option, buy longer-term option at same strike

Delta Math:

Net Portfolio Delta = Σ(Option Delta × Position Size × 100)

Aim for |Net Delta| < 10 for typical retail account sizes

Live Example: Iron Condor on SPY

Sell 450 Call

-1

+0.25

-25

Buy 455 Call

+0.15

+15

Sell 425 Put

-1

-0.30

+30

Buy 420 Put

-0.20

-20

Total

Key: Net delta of 0 = delta-neutral position. Profit comes from theta decay, not price movement.

Advantages

Low directional risk exposure
Consistent income from time decay
Works well in sideways markets
Easier to manage psychologically

Challenges

Requires frequent rebalancing
Vega risk (volatility spikes hurt)
Lower profit potential than directional plays
Higher transaction costs

Delta Hedging for Stock Portfolios

Risk Management

The Insurance Policy Approach

Use options to protect stock portfolios against adverse moves. The hedge ratio is determined by delta.

Hedge Calculation:

Number of Puts Needed = (Portfolio Beta × Portfolio Value × Target Hedge %) ÷ (Put Delta × 100 × Stock Price)

Common Hedging Scenarios:

1. Protective Put (Full Hedge)

Buy ATM puts with delta ≈ -0.50. For 100 shares (delta +100), buy 2 puts with delta -0.50 each = net delta 0.

2. Collar (Cost-Neutral Hedge)

Buy OTM put (delta ≈ -0.30) + Sell OTM call (delta ≈ +0.30). Premiums offset, creating “free” insurance.

3. Dynamic Hedge (Professional)

Adjust hedge size as delta changes. More puts when market drops, fewer when it rallies.

Hedge Calculator

Portfolio Value ($):

Portfolio Beta:

Put Delta:

Stock Price ($):

Hedge %: 50%

Result:

You need 13.33 put options to hedge 50% of your portfolio risk.

(Round to 13 contracts in practice)

Ratio Spreads & Delta Plays

Directional Bias

The Delta Gradient Strategy

Create positions with controlled, non-linear delta exposure to capitalize on expected price movements while defining risk.

Backspread (Long Gamma)

Example: Buy 2 ATM calls, Sell 1 ITM call.
Delta: Initially positive but increases rapidly if stock rises (positive gamma).
Use: When expecting large move, direction known.

Frontspread (Short Gamma)

Example: Sell 2 OTM calls, Buy 1 ATM call.
Delta: Initially negative but becomes more negative if stock drops.
Use: When expecting stock to stay below a level.

Delta Risk Profile:

Bullish Backspread

Initial Δ: +0.40

If ↑ 5%: Δ → +0.80

Bearish Frontspread

Initial Δ: -0.30

If ↓ 5%: Δ → -0.60

Professional Tips:

Gamma Matters: Ratio spreads have significant gamma – your delta exposure changes quickly with price moves.
Pin Risk: Be extremely careful around expiration with short options in ratio spreads.
Management: Have a plan to adjust or close if delta moves beyond your comfort zone.
Capital: These strategies often require substantial buying power due to undefined risk on one side.

<<<<<<<<<<<<>>>>>>>>>>>>>>>>

Conclusion

Ultimately, delta is the essential bridge between owning an option and understanding its behavior as a surrogate for the underlying asset. It provides a quantified measure of directional risk, a framework for strategic hedging, and a lens through which to view market probability. As we’ve explored, while powerful, it is not a standalone tool; its limitations, particularly its relationship with gamma, mean it must be used in conjunction with the other Greeks for a complete risk picture.

By actively monitoring the delta of your individual positions and your overall portfolio, you transition from gambling on price direction to managing a book of calculated risks. Start by checking the delta on your broker’s platform for your next potential trade—it will instantly clarify the bet you are making.

Ready to manage your portfolio’s delta like a pro? The right brokerage platform is critical. We recommend starting with a platform that offers comprehensive Greeks analytics and low-cost options trading. For an in-depth, independent comparison of the best brokers for active options traders, including reviews of platforms like Tastyworks and E*TRADE, visit a trusted resource like The Balance’s guide to options brokers.

How Delta Relates to Other Greeks

Feature	Delta (Δ)	Gamma (Γ)
What it Measures	Price sensitivity of the option to the underlying asset.	Rate of change of Delta itself.
Analogy	Speed of the option’s price.	Acceleration of the option’s price.
Primary Risk	Directional Risk (being right/wrong on the market move).	Convexity Risk (the speed of your P/L changing unexpectedly).
Highest When	Delta change is greatest for At-The-Money (ATM) options.	At-the-money (ATM) and near expiration.
Impact on Hedging	Determines the initial hedge ratio (# of shares to buy/sell).	Determines how often the hedge must be adjusted (dynamic hedging).

Related Terms

Gamma (Γ): As discussed, it’s the derivative of delta. Understanding gamma is non-negotiable for managing a delta-hedged portfolio.
Theta (Θ): Measures time decay—the loss in an option’s value as each day passes. There’s often a trade-off between positive delta and negative theta in directional strategies.
Vega (ν): Measures sensitivity to changes in implied volatility. Delta-neutral traders often have significant vega exposure.
Beta (β): While a different concept (from CAPM), both beta and delta measure sensitivity. Beta measures a stock’s sensitivity to the overall market, while delta measures an option’s sensitivity to its stock.

<<<<<<<<<<<<>>>>>>>>>>>>>>>>

Frequently Asked Questions

Can delta be greater than 1 or less than -1?

Yes, in certain scenarios. For deep in-the-money call options on highly volatile or leveraged assets (like some ETFs or futures contracts), delta can exceed 1.0. For example, a deep ITM call on a leveraged 3x ETF might have a delta of 1.5, meaning its price moves $1.50 for every $1 move in the ETF. This is because the option’s leverage compounds with the underlying asset’s leverage.

How does dividend issuance affect the delta of my options?

Significantly, and it’s often overlooked. As a stock goes ex-dividend, its price is expected to drop by roughly the dividend amount. This expectation is priced into options. For call holders, this makes the call slightly less valuable as the expected forward price is lower, which can slightly reduce its delta before the ex-date. For put holders, the opposite is true. This is a key consideration for delta-based hedging around dividend dates.

I’m a long-term investor writing covered calls. Should I worry about delta?

Absolutely. Your covered call position (long 100 shares, delta +1.0 each; short 1 call, delta say -0.30) has a net delta of +70. This is less bullish than owning the stock alone. If the stock surges past your strike, your call’s delta will approach -1.0, capping your upside (net delta ~0). Monitoring delta helps you understand how much participation you have in a rally and when it might be optimal to “roll” your call to a higher strike.

How do market makers use delta, and why does that affect the liquidity I see?

Market makers aim to be delta-neutral. When you buy a call from them, they become short delta. To hedge, they immediately buy shares of the underlying stock. Large orders can thus cause immediate buying or selling pressure in the stock itself—a phenomenon called “delta-driven flow.” This is why you might see a stock tick up slightly on a large options buy order, even before any news.

Is the “delta probability” a reliable guide for selling options for income?

It’s a starting point, but not reliable on its own. Selling a 0.30 delta put has a ~70% probability of success *according to the model*. However, this assumes constant volatility and a normal distribution of returns—both of which are false. Tail events (black swans) happen more often than the model predicts. Successful sellers use delta as a filter but combine it with fundamental analysis, support/resistance levels, and strict risk management (position sizing, stops).

Recommended Resources

Gamma: The Accelerator of Options Profits
Theta Decay: The Silent Partner in Options Trading
CBOE Options Education: The Chicago Board Options Exchange’s learning center is the definitive source for foundational options knowledge.
Natenberg’s Option Volatility and Pricing: This is the industry bible for understanding the Greeks and derivative pricing models.

Muhammad Faraz

Administrator

Faraz breaks down stocks, forex, commodities, and crypto with technical analysis, spotting key trends and trades daily. He specializes in technical and sentiment analysis, decoding complex market trends across crypto, forex, and stocks. With a sharp eye for key levels and breakout patterns, he transforms data into actionable trade setups.

Author's website Author's posts

Summary Table

What is Delta

Key Takeaways

The Core Concept Explained

How is Delta Calculated

Understanding the Components

Delta Across Different Asset Classes

Equity Options

Index Options (SPX, NDX)

Futures Options

Special Cases Worth Noting:

Currency (FX) Options

Crypto Options

Why Delta Matters to Traders and Investors

How to Use Delta in Your Trading Strategy

Advanced Delta Concepts: Charm, Color, and Beyond

Charm (Δ-Decay)

Real-World Impact:

Charm Formula (Call Option):

Color (Γ-Decay)

Trading Implications:

Professional Insight:

Practical Applications for Retail Traders

Hedge Timing

Position Selection

Risk Assessment

Delta in the Real World

Delta-Based Trading Strategies: From Theory to Practice

Delta-Neutral Trading

Core Concept

Implementation

Delta Math:

Live Example: Iron Condor on SPY

Advantages

Challenges

Delta Hedging for Stock Portfolios

The Insurance Policy Approach

Hedge Calculation:

Common Hedging Scenarios:

1. Protective Put (Full Hedge)

2. Collar (Cost-Neutral Hedge)

3. Dynamic Hedge (Professional)

Hedge Calculator

Result:

Ratio Spreads & Delta Plays

The Delta Gradient Strategy

Backspread (Long Gamma)

Frontspread (Short Gamma)

Delta Risk Profile:

Professional Tips:

Implementation Checklist:

Conclusion

How Delta Relates to Other Greeks

Related Terms

Frequently Asked Questions

Recommended Resources

About the Author

Related Stories

You may have missed